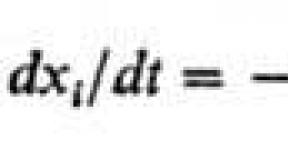Цели урока:

общеобразовательные:

• проверить теоретические знания учащихся (свойства прямоугольного треугольника, теорема Пифагора), умение использовать их при решении задач;
• создав проблемную ситуацию, подвести учащихся к “открытию” обратной теоремы Пифагора.

развивающие:

• развитие умений применять теоретические знания на практике;
• развитие умения формулировать выводы при наблюдениях;
• развитие памяти, внимания, наблюдательности:
• развитие мотивации учения через эмоциональное удовлетворение от открытий, через введение элементов истории развития математических понятий.

воспитательные:

• воспитывать устойчивый интерес к предмету через изучение жизнедеятельности Пифагора;
• воспитание взаимопомощи и объективного оценивания знаний одноклассников через взаимопроверку.

Форма урока: классно-урочная.

План урока:

• Организационный момент.
• Проверка домашнего задания. Актуализация знаний.
• Решение практических задач с использованием теоремы Пифагора.
• Новая тема.
• Первичное закрепление знаний.
• Домашнее задание.
• Итоги урока.
• Самостоятельная работа (по индивидуальным карточкам с отгадыванием афоризмов Пифагора).

Ход урока.

Организационный момент.

Проверка домашнего задания. Актуализация знаний.

Учитель: Какое задание вы выполняли дома?

Ученики: По двум данным сторонам прямоугольного треугольника найти третью сторону, ответы оформить в виде таблицы. Повторить свойства ромба и прямоугольника. Повторить, что называется условием, а что заключением теоремы. Подготовить сообщения о жизни и деятельности Пифагора. Принести веревку с 12-ю завязанными на ней узлами.

Учитель: Ответы к домашнему заданию проверьте по таблице

(черным цветом выделены данные, красным – ответы).

Учитель: На доске записаны утверждения. Если вы согласны с ними на листочках напротив соответствующего номера вопроса поставьте “+”, если не согласны, то поставьте “–”.

На доске заранее написаны утверждения.

1. Гипотенуза больше катета.
2. Сумма острых углов прямоугольного треугольника равна 180 0 .
3. Площадь прямоугольного треугольника с катетами а и в вычисляется по формуле S=ab/2 .
4. Теорема Пифагора верна для всех равнобедренных треугольников.
5. В прямоугольном треугольнике катет, лежащий напротив угла 30 0 , равен половине гипотенузы.
6. Сумма квадратов катетов равна квадрату гипотенузы.
7. Квадрат катета равен разности квадратов гипотенузы и второго катета.
8. Сторона треугольника равна сумме двух других сторон.

Проверяются работы с помощью взаимопроверки. Утверждения, вызвавшие споры, – обсуждаются.

Ключ к теоретическим вопросам.

Учащиеся ставят друг другу оценки по следующей системе:

8 правильных ответов “5”;
6-7 правильных ответов “4”;
4-5 правильных ответов “3”;
меньше 4 правильных ответов “2”.

Учитель: О чем мы говорили на прошлом уроке?

Ученик: О Пифагоре и его теореме.

Учитель: Сформулируйте теорему Пифагора. (Несколько учеников читают формулировку, в это время 2-3 ученика доказывают ее у доски, 6 учеников – за первыми партами на листочках).

На магнитной доске на карточках написаны математические формулы. Выберите те из них, которые отражают смысл теоремы Пифагора, где а и в – катеты, с – гипотенуза.

Пока учащиеся, доказывающие теорему у доски и на местах, не готовы, слово предоставляется тем, кто подготовил сообщения о жизни и деятельности Пифагора.

Школьники, работающие на местах, сдают листочки и слушают доказательства тех, кто работал у доски.

Учитель: предлагаю вам практические задачи с применением изучаемой теоремы. Побываем сначала в лесу, после бури, потом на загородном участке.

Задача 1 . После бури сломалась ель. Высота оставшейся части 4,2 м. Расстояние от основания до упавшей макушки 5,6 м. Найти высоту ели до бури.

Задача 2 . Высота дома 4,4 м Ширина газона вокруг дома 1,4 м. Какой длины надо изготовить лестницу, чтобы она не заступала на газон и доставала до крыши дома?

Учитель: (звучит музыка) Закройте глаза, на несколько минут мы окунемся в историю. Мы с вами в Древнем Египте. Вот на верфях египтяне строят свои знаменитые корабли. А вот землемеры, они измеряют участки земли, границы которых смылись после разлива Нила. Строители строят грандиозные пирамиды, которые до сих пор поражают нас своим великолепием. Во всех этих видах деятельности египтянам необходимо было использовать прямые углы. Они умели строить их с помощью веревки с 12 ю завязанными на одинаковом расстоянии друг от друга узелками. Попробуйте и вы, рассуждая как древние египтяне, построить с помощью своих веревок прямоугольные треугольники. (Решая эту проблему, ребята работают в группах по 4 человека. Через некоторое время на планшете у доски кто-то показывает построение треугольника).

Стороны полученного треугольника 3, 4 и 5. Если между этими узлами завязать еще по одному узлу, то его стороны станут 6, 8 и 10. Если по два – 9, 12 и 15. Все эти треугольники являются прямоугольными т. к.

5 2 = 3 2 + 4 2 , 10 2 = 6 2 + 8 2 , 15 2 = 9 2 + 12 2 и т.д.

Каким свойством должен обладать треугольник, чтобы быть прямоугольным? (Учащиеся пытаются сами сформулировать обратную теорему Пифагора, наконец, у кого-то это получается).

Чем эта теорема отличается от теоремы Пифагора?

Ученик: Условие и заключение поменялись местами.

Учитель: Дома вы повторяли, как называются такие теоремы. Так с чем мы сейчас познакомились?

Ученик: С обратной теоремой Пифагора.

Учитель: Запишем в тетради тему урока. Откройте учебники на стр. 127 прочитайте еще раз это утверждение, запишите его себе в тетрадь и разберите доказательство.

(После нескольких минут самостоятельной работы с учебником по желанию один человек у доски приводит доказательство теоремы).

1. Как называется треугольник со сторонами 3, 4 и 5? Почему?
2. Какие треугольники называются пифагоровыми?
3. С какими треугольниками вы работали в домашнем задании? А в задачах с сосной и лестницей?

Эта теорема помогает решать задачи, в которых надо выяснить, будут ли треугольники прямоугольными.

Задания:

1) Выясните, является ли треугольник прямоугольным, если его стороны равны:

а) 12,37 и 35; б) 21, 29 и 24.

2) Вычислите высоты треугольника со сторонами 6, 8 и 10 см.

Стр.127:обратная теорема Пифагора. № 498(а,б,в) № 497.

Самостоятельная работа (проводится по индивидуальным карточкам).

Учитель: Дома вы повторяли свойства ромба и прямоугольника. Перечислите их (идет беседа с классом). На прошлом уроке мы говорили о том, что Пифагор был разносторонней личностью. Он занимался и медициной, и музыкой, и астрономией, а так же был спортсменом и участвовал в олимпийских играх. А еще Пифагор был философом. Многие его афоризмы и сегодня актуальны для нас. Сейчас вы будете выполнять самостоятельную работу. К каждому заданию дано несколько вариантов ответов, рядом с которыми записаны фрагменты афоризмов Пифагора. Ваша задача – решив все задания, составить из полученных фрагментов высказывание и записать его.

Теорема Пифагора гласит:

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы:

a 2 + b 2 = c 2 ,

• a и b – катеты, образующие прямой угол.
• с – гипотенуза треугольника.

Формулы теоремы Пифагора

• a = \sqrt{c^{2} - b^{2}}
• b = \sqrt {c^{2} - a^{2}}
• c = \sqrt {a^{2} + b^{2}}

Доказательство теоремы Пифагора

Площадь прямоугольного треугольника вычисляется по формуле:

S = \frac{1}{2} ab

Для вычисления площади произвольного треугольника формула площади:

• p – полупериметр. p=\frac{1}{2}(a+b+c) ,
• r – радиус вписанной окружности. Для прямоугольникаr=\frac{1}{2}(a+b-c).

Потом приравниваем правые части обеих формул для площади треугольника:

\frac{1}{2} ab = \frac{1}{2}(a+b+c) \frac{1}{2}(a+b-c)

2 ab = (a+b+c) (a+b-c)

2 ab = \left((a+b)^{2} -c^{2} \right)

2 ab = a^{2}+2ab+b^{2}-c^{2}

0=a^{2}+b^{2}-c^{2}

c^{2} = a^{2}+b^{2}

Обратная теорема Пифагора:

Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный. То есть для всякой тройки положительных чисел a, b и c , такой, что

a 2 + b 2 = c 2 ,

существует прямоугольный треугольник с катетами a и b и гипотенузой c .

Теорема Пифагора - одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Доказана она ученым математиком и философом Пифагором.

Значение теоремы в том, что с ее помощью можно доказать другие теоремы и решать задачи.

Дополнительный материал:

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение

между сторонами прямоугольного треугольника .

Считается, что доказана греческим математиком Пифагором, в честь которого и названа.

Геометрическая формулировка теоремы Пифагора.

Изначально теорема была сформулирована следующим образом:

В прямоугольном треугольнике площадь квадрата , построенного на гипотенузе , равна сумме площадей квадратов ,

построенных на катетах.

Алгебраическая формулировка теоремы Пифагора.

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

То есть, обозначив длину гипотенузы треугольника через c , а длины катетов через a и b :

Обе формулировки теоремы Пифагора эквивалентны, но вторая формулировка более элементарна, она не

требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и

измерив только длины сторон прямоугольного треугольника .

Обратная теорема Пифагора.

Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то

треугольник прямоугольный.

Или, иными словами:

Для всякой тройки положительных чисел a , b и c , такой, что

существует прямоугольный треугольник с катетами a и b и гипотенузой c .

Теорема Пифагора для равнобедренного треугольника.

Теорема Пифагора для равностороннего треугольника.

Доказательства теоремы Пифагора.

На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема

Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие

можно объяснить лишь фундаментальным значением теоремы для геометрии.

Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них:

доказательства методом площадей , аксиоматические и экзотические доказательства (например,

с помощью дифференциальных уравнений ).

1. Доказательство теоремы Пифагора через подобные треугольники.

Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся

напрямую из аксиом. В частности, оно не использует понятие площади фигуры.

Пусть ABC есть прямоугольный треугольник с прямым углом C . Проведём высоту из C и обозначим

её основание через H .

Треугольник ACH подобен треугольнику AB C по двум углам. Аналогично, треугольник CBH подобен ABC .

Введя обозначения:

получаем:

,

что соответствует -

Сложив a 2 и b 2 , получаем:

или , что и требовалось доказать.

2. Доказательство теоремы Пифагора методом площадей.

Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они

используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.

• Доказательство через равнодополняемость.

Расположим четыре равных прямоугольных

треугольника так, как показано на рисунке

справа.

Четырёхугольник со сторонами c - квадратом,

так как сумма двух острых углов 90°, а

развёрнутый угол — 180°.

Площадь всей фигуры равна, с одной стороны,

площади квадрата со стороной (a+b ), а с другой стороны, сумме площадей четырёх треугольников и

Что и требовалось доказать.

3. Доказательство теоремы Пифагора методом бесконечно малых.

​

Рассматривая чертёж, показанный на рисунке, и

наблюдая изменение стороны a , мы можем

записать следующее соотношение для бесконечно

малых приращений сторон с и a (используя подобие

треугольников):

Используя метод разделения переменных, находим:

Более общее выражение для изменения гипотенузы в случае приращений обоих катетов:

Интегрируя данное уравнение и используя начальные условия, получаем:

Таким образом, мы приходим к желаемому ответу:

Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной

пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми

вкладами от приращения разных катетов.

Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения

(в данном случае катет b ). Тогда для константы интегрирования получим:

Рассмотрение тем школьной программы с помощью видеоуроков является удобным способом изучения и усвоения материала. Видео помогает сконцентрировать внимание учащихся на основных теоретических положениях и не упускать важных деталей. При необходимости школьники всегда могут прослушать видеоурок повторно или вернуться на несколько тем назад.

Данный видеоурок для 8-го класса поможет учащимся изучить новую тему по геометрии.

В предыдущей теме мы изучили теорему Пифагора и разобрали ее доказательство.

Существует также теорема, которая известна как обратная теорема Пифагора. Рассмотрим ее подробнее.

Теорема. Треугольник является прямоугольным, если в нем выполняется равенство: значение одной стороны треугольника, возведенной в квадрат, такое же, как сумма возведенных в квадрат двух других сторон.

Доказательство. Допустим, нам дан треугольник ABC, в котором выполняется равенство AB 2 = CA 2 + CB 2 . Необходимо доказать, что угол С равен 90 градусов. Рассмотрим треугольник A 1 B 1 C 1 , в котором угол С 1 равен 90 градусов, сторона C 1 A 1 равна CA и сторона B 1 C 1 равна BС.

Применяя теорему Пифагора, запишем отношение сторон в треугольнике A 1 C 1 B 1: A 1 B 1 2 = C 1 A 1 2 + C 1 B 1 2 . Произведя замену в выражении на равные стороны, получим A 1 B 1 2 = CA 2 + CB 2 .

Из условий теоремы мы знаем, что AB 2 = CA 2 + CB 2 . Тогда можем записать A 1 B 1 2 = AB 2 , из чего следует, что A 1 B 1 = AB.

Мы нашли, что в треугольниках ABC и A 1 B 1 C 1 равны три стороны: A 1 C 1 = AC, B 1 C 1 = BC, A 1 B 1 = AB. Значит, эти треугольники равны. Из равенства треугольников следует, что угол С равен углу С 1 и соответственно равен 90 градусов. Мы определили, что треугольник ABC прямоугольный и его угол С равен 90 градусов. Мы доказали данную теорему.

Далее автор приводит пример. Допустим, дан произвольный треугольник. Известны размеры его сторон: 5, 4 и 3 единиц. Проверим утверждение из теоремы, обратной теореме Пифагора: 5 2 = 3 2 + 4 2 . Утверждение верно, значит данный треугольник прямоугольный.

В следующих примерах треугольники также будут прямоугольными, если их стороны равны:

5, 12, 13 единиц; равенство 13 2 = 5 2 + 12 2 является верным;

8, 15, 17 единиц; равенство 17 2 = 8 2 + 15 2 является верным;

7, 24, 25 единиц; равенство 25 2 = 7 2 + 24 2 является верным.

Известно понятие пифагорового треугольника. Это прямоугольный треугольник, у которого значения сторон равны целым числам. Если катеты пифагорового треугольника обозначить через a и c, а гипотенузу b, то значения сторон этого треугольника можно записать с помощью следующих формул:

b = k x (m 2 - n 2)

c = k x (m 2 + n 2)

где m, n, k- любые натуральные числа, причем значение m больше значения n.

Интересный факт: треугольник со сторонами 5, 4 и 3 называют также египетским треугольником, такой треугольник был известен еще в Древнем Египте.

В данном видеоуроке мы ознакомились с теоремой, обратной теореме Пифагора. Подробно рассмотрели доказательство. Также учащиеся узнали, какие треугольники называют пифагоровыми.

Учащиеся с легкостью могут ознакомиться с темой «Теорема, обратная теореме Пифагора» самостоятельно с помощью данного видеоурока.